Modern self-optimization of ultrashort pulses
On: Nov 02, 2022
In: Ultrafast Lasers
Introduction
Short-pulse lasers are used in countless applications, including in material processing, refractive surgery, multi-photon imaging, semiconductor inspection, and a host of scientific uses. For laser manufacturers, this great diversity encourages the development of flexible technology platforms that must be configured according to the needs of end users. Managing this flexibility and these various configurations is often a challenge; in fact, several factors can complicate achieving the target performance in the desired operating ranges. How do you find the optimal adjustments for each unit to be produced with acceptable yields, lead times and costs? How do you ensure that the pulse will have the characteristics requested by the user at such or such a repetition rate?
This white paper discusses the potential of TeraXion's Tunable Pulse Stretcher (TPSR) to obtain optimal pulses automatically with short-pulse lasers based on Chirped Pulse Amplification (CPA).
A reminder about the principle of CPA systems
The CPA-type fiber laser architecture used to generate the results presented in this paper is illustrated in a simplified manner in Figure 1. This is a classic configuration that allows a laser pulse to be temporally broadened (with the help of a TPSR here) in order to increase its energy without risking reaching excessively high peak powers likely to generate non-linear effects that can compromise the pulse quality and even the integrity of the amplifier chain. The final step consists in recompressing the pulse, in free-space propagation, to restore its minimum duration.
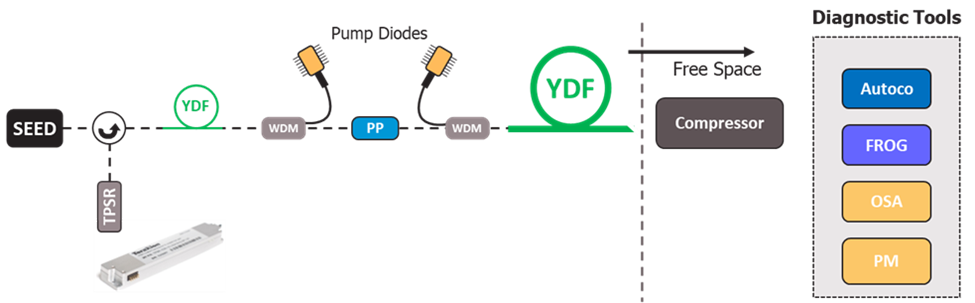
Figure 1. Schematic representation of the fiber CPA laser used to generate the results presented in this paper. OSC: master oscillator, YDF: Yb-doped fiber, WDM: pump coupler, PP: pulse picker, Autoco: autocorrelator, FROG: Frequency Resolved Optical Gating, OSA: optical spectral analyzer, PM: power meter.
Fundamentally, maintaining pulse quality involves ensuring that the stretcher dispersion cancels out the compressor dispersion, plus any other contribution from a physical phenomenon related to the propagation of the pulse in the optical chain. In order to bring out this notion of balance, we can focus on the phase of the pulse propagating in our laser. This can be broken down into a Taylor series [1], and thus reveal the dispersion coefficients β2, β3, and so on,
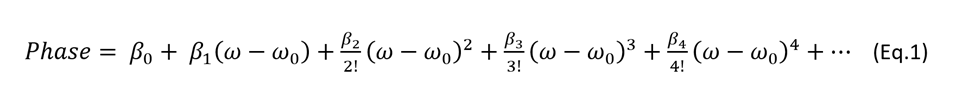
Thus, without any nonlinear effect, the phases induced by each of the laser’s components cancel each other out:
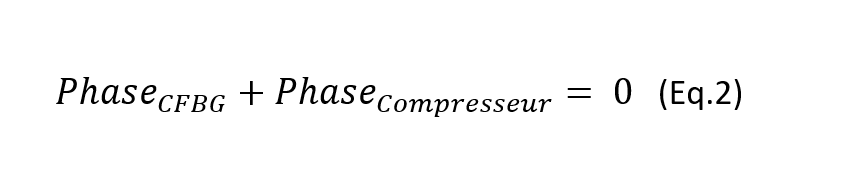
It is worth noting that there is a phase induced by the dispersion of the fiber, PhasePropagation, corresponding mainly to the fiber’s Group-Velocity Dispersion (GVD). It is usually extremely low, on the order of a few percent of PhaseTPSR. Also, the TPSR is normally designed to pre-compensate for this phase, which is why it is not shown here. In a real situation, several conditions can compromise the maintenance of the desired balance, in particular the operation in a non-linear regime (contribution of the self-phase modulation (SPM)), the tolerances of the optical components, and the compressor alignment. It is under these conditions that the TPSR phase’s tunability becomes a major asset, as it now makes it possible to overcome these normally limiting effects on CPA systems.
Automatic pulse quality optimization with a tunable pulse stretcher (TPSR)
In order to illustrate the possibilities provided by the TPSR, we can start by analyzing a pulse that has not been properly optimized, whose final (spectral) phase is not zero. This may be due to components whose phases do not cancel each other out. Figure 2A) represents the temporal and spectral profile of a pulse measured via a FROG (Frequency Resolved Optical Gating) [2]. As can be seen on the temporal profile, the pulse has a duration of around 1.2 ps while the width of its spectrum could provide a Fourier transform-limited (TFL) duration around 355 fs. This difference comes from the non-zero spectral phase represented in red on the right graph of Figure 2A).
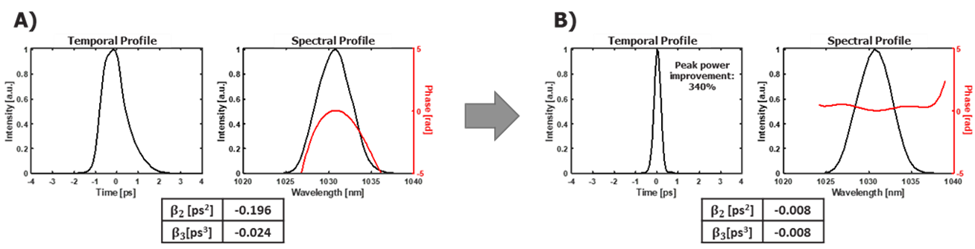
Figure 2. Temporal and spectral profiles (curves in black) and spectral phases (curves in red) of an uncompressed pulse, found by a FROG measurement, A) before and B) after optimization with the TPSR using the Nelder Mead method.
In order to approach the Fourier limit, this phase must be cancelled either by realigning the compressor or by adjusting the TPSR. From a technical point of view, the compressor can be adjusted by modifying the internal propagation distance and/or by adjusting the beam’s angle of incidence. However, these adjustments require laborious work that is done in free space propagation and dependent upon rotating mechanical mounts having their tolerances and reliability. Moreover, in a grating compressor, the adjustments will modify β2 and β3 in a co-dependent way, which limits this method’s precision and room for maneuver. Compensation with the TPSR makes it possible to play finely and independently on the ω0, β2, and β3 parameters, which make up the phase of equation (1), without resorting to moving parts.
In the example that interests us here, cancelling the residual phase involves adding variations on the TPSR so that β2 = -0.196 ps2 and β3 = -0.24 ps3. In order to find the TPSR’s ideal adjustment in a simple way, a multivariate optimization algorithm was used: the Nelder-Mead method [3]. This makes it possible to optimize each coefficient of equation (1) with the objective of reducing the duration of the measured pulse (or increasing the peak power, depending upon the chosen measurement tool).
If we return to the pulse presented earlier (Fig. 2A)), and optimize the TPSR via the Nelder-Mead method, a compressed pulse very close to its TFL, as presented in Fig. 2B), is obtained by less than 4 minutes, without human intervention. Despite this optimization, the pulse is not perfect and the phase presented on the right curve is not zero. However, the values of the residual coefficients have decreased by more than an order of magnitude.
Compensation for compressor misalignment
If the compressor is not perfectly aligned with the optimum grating distance and angles, the balance of equation (2) no longer holds, and the pulse will be sub-optimal. It is therefore necessary to compensate for this variation, which jeopardizes the initial balance. In the following paragraphs we will show that the TPSR can automatically compensate for compressor misalignment in a few minutes.
Let’s start by doing our best to position our compressor at its optimal angle: θ0=62.97°, which corresponds to the TPSR design’s nominal angle. But with imperfect alignment and non-linear effects, the pulse compression is not perfect, as shown in Figure 3A). As for FIG. 2, the temporal profiles are represented on the left and the spectral profiles, as well as their phase, on the right. Note that this time the FROG trace is also present. The asymmetrical rebounds of this temporal profile suggest that the TOD (Third Order Dispersion) is the major contributor. In fact, the pulse seems quite short in time, and will only require a slight adjustment on the β2. Figure 3B) presents the pulse after the TPSR’s optimization via the Nelder-Mead method. The temporal profile is much more symmetrical and has only a very weak pedestal. The residual phase is much flatter, and the residual β2 and β3 coefficients have strongly decreased, which confirms pulse optimization.
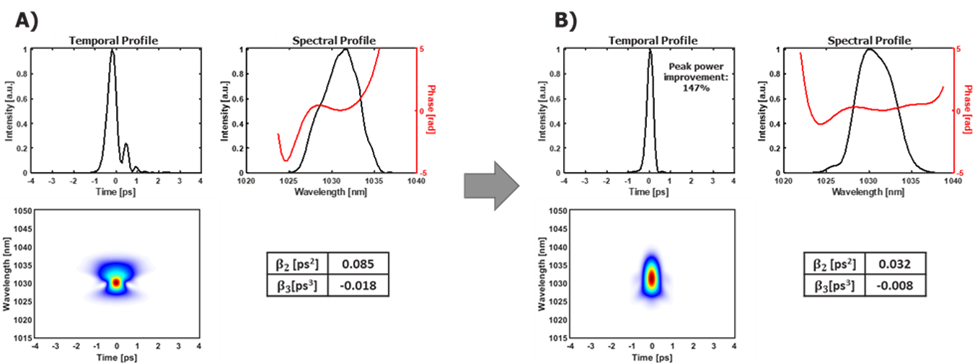
Figure 3. Temporal and spectral profiles (curves in black), spectral phases (curves in red) and FROG traces of an uncompressed pulse, found by a FROG measurement, A) before and B) after optimization with the TPSR using the Nelder-Mead method, with the compressor aligned at its optimal angle (62.97°).
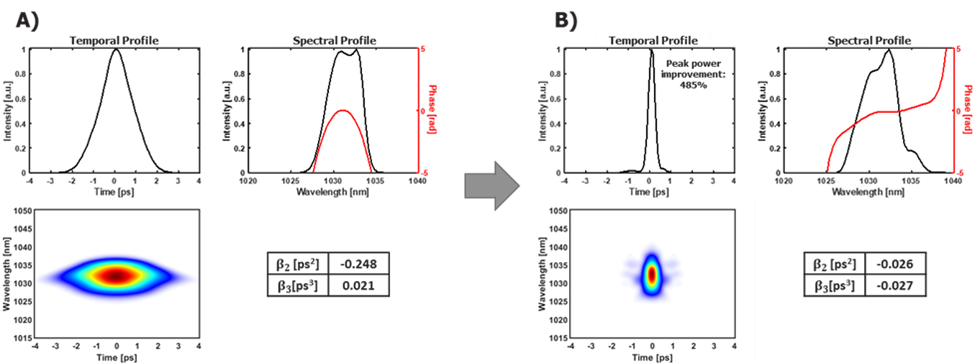
Figure 4. Temporal and spectral profiles (curves in black), spectral phases (curves in red) and FROG traces of an uncompressed pulse, found by a FROG measurement, A) before and B) after optimization with the TPSR using the Nelder-Mead method, with the compressor misaligned by -0.06° from its optimum angle.
The pulse is therefore optimized for an initial compressor position. We are now going to force a misalignment of this one, by rotating the gratings. The initial angle, θ0, will be reduced by 0.06°. This rotation changes the compressor’s parameters and the balance of equation (2) is broken. The pulse is directly impacted, as shown in Figure 4A). Its duration is greatly extended, and its spectral phase is far from zero. Again, the TPSR can be used to optimize it via the Nelder-Mead method. The result is shown in Figure 4B). An equally convincing result (not shown here) was obtained by applying this method for an angular misalignment of +0.06°.
Conclusion
The few examples presented in this white paper demonstrate the potential of TeraXion's Tunable Pulse Stretcher (TPSR) to obtain optimal pulses automatically with short pulse lasers based on Chirped Pulse Amplification (CPA). The method discussed here can be adapted for the purposes of laser assembly production and provide several benefits. Compared to traditional trial-and-error approaches, this method saves time in achieving optimum pulse quality and reduces the need for highly trained personnel. Distortions resulting from the variability of the optical components’ characteristics and manufacturing processes can be quickly compensated. The finesse of the TPSR’s phase control suggests exploring even more advanced automation solutions, based for example on machine learning, to compensate for phase variations from various origins. Do not miss our examples of typical automation in one of our next publications on the subject.
We invite you to contact TeraXion if you have any projects or needs associated with automating the pulse quality of short-pulsed lasers. We will be happy to discuss it with you and explore new ideas.
Bibliography
[1] G. P. Agrawal, Nonlinear fiber optics. Elsevier Science, 2013.
[2] D. J. Kane and R. Trebino, “Characterization of arbitrary femtosecond pulses using frequency-resolved optical gating,” IEEE J. Quantum Electron., vol. 29, no. 2, pp. 571–579, 1993, doi: 10.1109/3.199311.
[3] J. A. Nelder and R. Mead, “A Simplex Method for Function Minimization,” Comput. J., vol. 7, no. 4, pp. 308–313, Jan. 1965, doi: 10.1093/COMJNL/7.4.308.
Tunable Pulse Stretcher for Ultrafast Lasers
The TPSR is specifically designed for the generation of ultrafast pulses.
